Standarta un parastā Excel sadalījuma aprēķini

NORM.DIST un NORM.S.DIST

ThoughtCo/Kortnija Teilore

Gandrīz jebkuru statistikas programmatūras pakotni var izmantot aprēķiniem attiecībā uz normālu sadalījumu, kas plašāk pazīstams kā zvana līkne. Programma Excel ir aprīkota ar daudzām statistikas tabulām un formulām, un ir diezgan vienkārši izmantot kādu no tās funkcijām normālam sadalījumam. Mēs redzēsim, kā programmā Excel izmantot funkcijas NORM.S.DIST un NORM.S.DIST.

Normālie sadalījumi

Ir bezgalīgs skaits normālo sadalījumu. Normālo sadalījumu nosaka noteikta funkcija, kurā ir noteiktas divas vērtības: vidējā un standarta novirze. Vidējais ir jebkurš reāls skaitlis, kas norāda sadalījuma centru. Standarta novirze ir pozitīva reāls skaitlis tas ir sadalījuma izplatības mērījums. Kad mēs zinām vidējās un standarta novirzes vērtības, konkrētais normālais sadalījums, ko mēs izmantojam, ir pilnībā noteikts.

The standarta normālais sadalījums ir viens īpašs sadalījums no bezgalīga skaita normālo sadalījumu. Standarta normālā sadalījuma vidējais rādītājs ir 0 un standarta novirze 1. Jebkuru normālo sadalījumu var standartizēt standarta normālajam sadalījumam ar vienkāršu formulu. Tāpēc parasti vienīgais normālais sadalījums ar tabulā norādītajām vērtībām ir standarta normālais sadalījums. Šāda veida tabulas dažreiz tiek sauktas par z punktu tabulu.

NORM.S.DIST

Pirmā Excel funkcija, ko mēs pārbaudīsim, ir funkcija NORM.S.DIST. Šī funkcija atgriež standarta normālo sadalījumu. Funkcijai ir nepieciešami divi argumenti: Ar un kumulatīvi. Pirmais arguments par Ar ir standarta noviržu skaits no vidējā. Tātad, Ar = -1,5 ir pusotra standarta novirze zem vidējā. The Ar - rezultāts Ar = 2 ir divas standarta novirzes virs vidējā.

Otrais arguments ir kumulatīvs. Šeit var ievadīt divas iespējamās vērtības: 0 varbūtības blīvuma funkcijas vērtībai un 1 kumulatīvā sadalījuma funkcijas vērtībai. Lai noteiktu laukumu zem līkne , mēs vēlamies šeit ievadīt 1.

Piemērs

Lai palīdzētu saprast, kā šī funkcija darbojas, mēs apskatīsim piemēru. Ja noklikšķinām uz šūnas un ievadām =NORM.S.DIST(.25, 1), pēc ievadīšanas noklikšķināšanas šūnā būs vērtība 0.5987, kas ir noapaļota līdz četrām zīmēm aiz komata. Ko tas nozīmē? Ir divas interpretācijas. Pirmais ir tas, ka laukums zem līknes Ar mazāks par vai vienāds ar 0,25 ir 0,5987. Otrā interpretācija ir tāda, ka 59,87 procenti laukuma zem līknes standarta normālajam sadalījumam rodas, kad Ar ir mazāks vai vienāds ar 0,25.

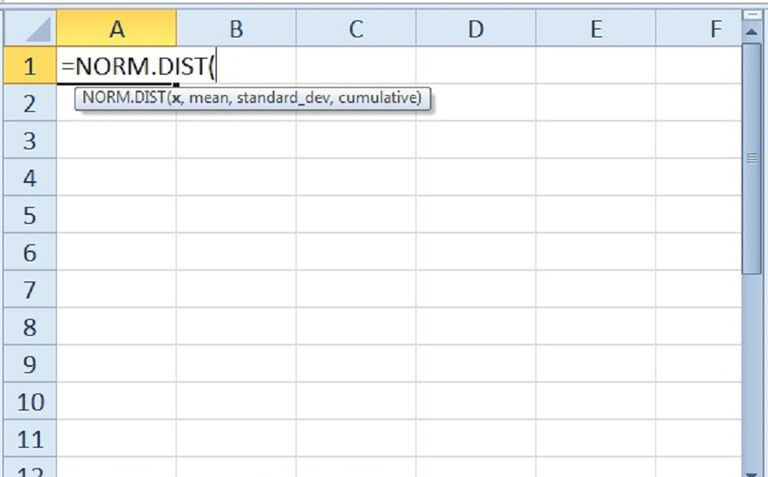
NORM.DIST

Otrā Excel funkcija, kuru mēs apskatīsim, ir funkcija NORM.DIST. Šī funkcija atgriež normālo sadalījumu noteiktai vidējai un standarta novirzei. Funkcijai ir nepieciešami četri argumenti: x , vidējā, standarta novirze un kumulatīvā vērtība. Pirmais arguments par x ir mūsu sadalījuma novērotā vērtība. Vidējais un standarta novirze ir pašsaprotami. Pēdējais kumulatīvās arguments ir identisks funkcijas NORM.S.DIST argumentam.

Piemērs

Lai palīdzētu saprast, kā šī funkcija darbojas, mēs apskatīsim piemēru. Noklikšķinot uz šūnas un ievadot =NORM.DIST(9, 6, 12, 1), pēc ievadīšanas šūnā būs vērtība 0,5987, kas ir noapaļota līdz četrām zīmēm aiz komata. Ko tas nozīmē?

Argumentu vērtības norāda, ka mēs strādājam ar normālo sadalījumu, kura vidējais rādītājs ir 6 un standarta novirze 12. Mēs cenšamies noteikt, cik procentuālais sadalījums rodas x mazāks par vai vienāds ar 9. Līdzvērtīgi mēs vēlamies laukumu zem šī konkrētā līknes normālais sadalījums un pa kreisi no vertikālās līnijas x = 9.

NORM.S.DIST vs NORM.DIST

Iepriekš minētajos aprēķinos ir jāņem vērā dažas lietas. Mēs redzam, ka rezultāts katram no šiem aprēķiniem bija identisks. Tas ir tāpēc, ka 9 ir par 0,25 standarta novirzēm virs vidējās 6. Mēs varējām vispirms konvertēt x = 9 uz a Ar -rezultāts 0,25, bet programmatūra to dara mūsu vietā.

Otra lieta, kas jāatzīmē, ir tā, ka mums tiešām nav vajadzīgas abas šīs formulas. NORM.S.DIST ir īpašs NORM.DIST gadījums. Ja vidējais rādītājs ir vienāds ar 0 un standarta novirze ir 1, tad NORM.DIST aprēķini sakrīt ar NORM.S.DIST aprēķiniem. Piemēram, NORM.DIST(2, 0, 1, 1) = NORM.S.DIST(2, 1).